- 教学
- 下载
- 作文
- 知识
- 课件
- 教案
概要:高中物理气压随高度的变化关系实验课题研究 1648年,帕斯卡和他的朋友在山顶和山脚下同时做了托里拆利实验,证实了大气压随高度而变化。通常,在海拔2千米以内,可以近似认为每升高12米,大气压降低1毫米汞柱。今天我们把托里拆利的实验装置搬到高楼或高山上去做实验是相当困难的,但是我们可以应用理想气体的定律,以较简便的装置来研究气压随高度的变化关系,同时还可以学到一种应用图线求某点高度的方法。 方案一应用气态方程的实验取一端封闭且粗细均匀的细玻璃管(约50—60厘米长),刻度尺,水银温度计(尽可能选准确度高的),注射针筒,水银气压计和少许水银备用。用注射器把少量水银注入一端封闭的玻璃管,并借助一根干净的细钢丝使这段水银柱停留在离管口8—10厘米处。在实验室里把玻璃管水平放置(用气泡水准器校正水平),测出玻璃管中被水银密封的空气柱的长度L0,如图(一)3.48-1所示,同时测出气温t0和实验室里大气压强的值P0。 然后把玻璃管和温度计等带到高楼的底层(或山脚下),仍然水平放置玻璃管,测出密封气柱的长度LA,以及当地的温度tA,由理想气体
高中物理气压随高度的变化关系实验课题研究,标签:高中物理实验,高中物理电学实验,http://www.wenxue9.com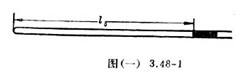 然后把玻璃管和温度计等带到高楼的底层(或山脚下),仍然水平放置玻璃管,测出密封气柱的长度LA,以及当地的温度tA,由理想气体的状态方程P0L0/T0=PALA/TA,可以求得A处的大气压强PA=L0TAP0/LAT0。同样在第6层楼、第12层楼、第18层楼等处(或者在山上几个已知相对高度的地点)分别重复上述实验测量步骤,算出相应的气压PB、PC……并根据楼层高度估算出B、C等层的高度。把你的测量数据记录在下列表中:
然后把玻璃管和温度计等带到高楼的底层(或山脚下),仍然水平放置玻璃管,测出密封气柱的长度LA,以及当地的温度tA,由理想气体的状态方程P0L0/T0=PALA/TA,可以求得A处的大气压强PA=L0TAP0/LAT0。同样在第6层楼、第12层楼、第18层楼等处(或者在山上几个已知相对高度的地点)分别重复上述实验测量步骤,算出相应的气压PB、PC……并根据楼层高度估算出B、C等层的高度。把你的测量数据记录在下列表中:地点
温度
气柱长度l(cm)
气柱
P0=L0TP0/lT0 (mmHg)
高度H
(m)
T(℃)
T(K)
O
A
B
C
D